Gå effektivt i fjellet
Hvor raskt kan du gå uten å bruke for mye energi?
En formel fra 1971 hjelper oss i alle fall et stykke på veien...
Bruker man mest energi på én kilometer om man går fort eller sakte?
Det er et stadig tilbakevendende spørsmål. Det koster selvsagt mindre energi å gå sakte enn fort, men samtidig bruker man lengre tid på distansen.
Matematisk formel
Om vi dykker ned i forskningens verden, finner vi at flere har forsøkt å sette opp matematiske formler for energiforbruket under marsj. En slik formel må åpenbart ta høyde for mange faktorer, som terreng, stigning, personens vekt og eventuell oppakning. Allerede i 1971 kom forskere med et forslag, se faktaboks.
LES OGSÅ: Sokkene som stopper mygg og flått
Passer rimelig bra
Denne formelen er et eksempel på en empirisk formel. Den har blitt til ved tilpasning til forsøk, ikke gjennom en fundamental beskrivelse av virkeligheten. Den observante leser vil blant annet se at den egentlig ikke gir et svar med enhet Watt. En slik ligning vil selvsagt aldri gi fullstendig korrekte svar for alle forhold, men den har vist seg å passe rimelig bra med forsøk i felt, og kan derfor være et bra verktøy for oss.
Tre ledd
Lange matematiske formler ser alltid skremmende ut, men denne er lettere å forstå om vi ser at den består av tre ledd, som her er farget rødt, blått og svart.
Det røde leddet inneholder kun én faktor: personens vekt. Det representerer derfor energiforbruket når vi står rolig.
Det blå leddet tar hensyn til personens og ryggsekkens vekt. Det representerer altså energiforbruk ved å stå rolig med oppakning.
Det siste leddet er mest interessant i denne sammenhengen. Her kommer hastigheten inn, og siden leddet inneholder kvadratet av hastigheten, vil energiforbruket øke stadig raskere med økende fart.
LES OGSÅ: Skal du fiske laks, må du beherske denne fisketeknikken
Men, det visste vi jo...
Når hastigheten er null, forsvinner siste ledd, og energiforbruk per sekund blir minst, men siden vi da aldri kommer noe sted, blir energiforbruk per kilometer uendelig stort.
Formel for energiforbruk
under marsj
M = 1,5W + 2,0(W+L)()2 + h(W+L)(1,5V〗2+0,35VG)
M = effekt (Watt)
W = personens vekt
L = ryggsekkens vekt
V = gangfart (m/s)
G = stigning (%)
h = terrengfaktor
Når hastigheten blir stor, vil det svarte leddet i ligningen bli dominerende, og siden det vokser med kvadratet av hastigheten, vil økningen i energiforbruk per sekund dominere over at vi samtidig bruker kortere tid på én kilometer.
Ett eller annet sted mellom null og uendelig finnes den ideelle hastigheten, men det kan man selvsagt innvende at vi visste fra før...
Svaret er 3,5 km/t
Den enkleste måten å finne den ideelle hastigheten på, er å multiplisere effekten vi får fra ligningen med tiden det tar å gå én kilometer.
Den finner vi ved å dele 1000 på hastigheten i meter per sekund. Resultatet er vist i grafen for en person på 70 kilo med 20 kilos oppakning som går på flatmark med hastigheter mellom 1 og 9 kilometer i timen.
Vi ser at formelen beregner energiforbruket til å være lavest ved ca. 3,5 kilometer i timen.
Behagelig tempo
Siste sjekkpunkt når man har brukt en slik formel, er å vurdere om svaret virker fornuftig, og det gjør det i høyeste grad her.
For min del føles i alle fall et gangtempo på snaut fire kilometer i timen som svært behagelig og effektivt.
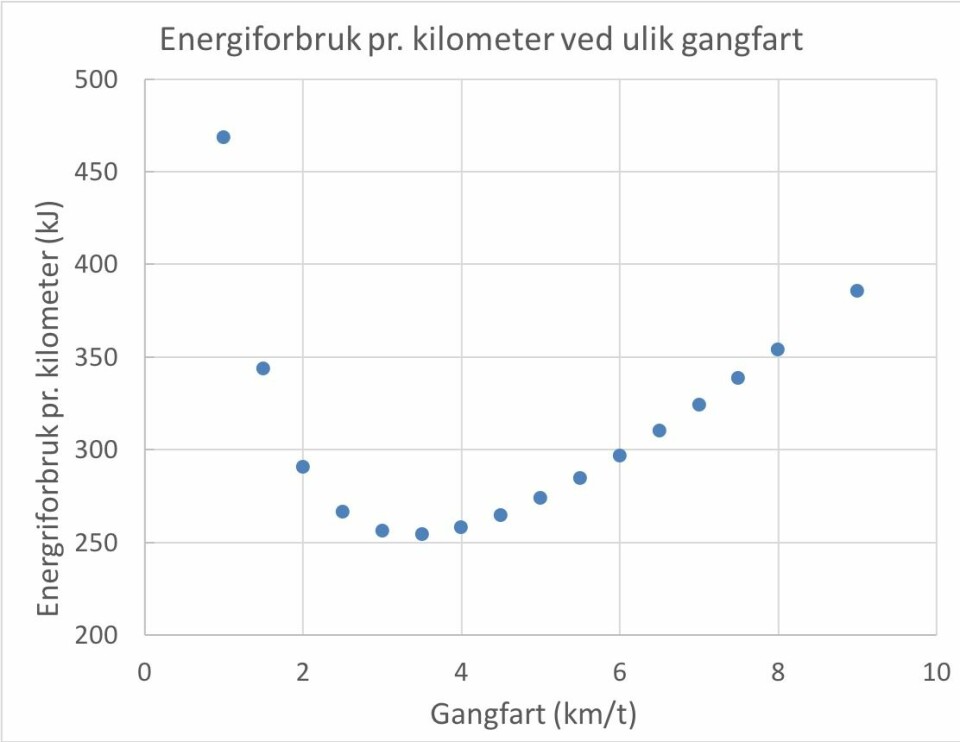
Et tempo på seks kilometer i timen betyr derimot at man må fokusere på å gå fort. Formelen anslår at det gir en økning i energiforbruk per kilometer på ca. 17 %.
Kilde: Giovanni og Goldman: Predicting metabolic energy cost. Journal of Applied Physiology, 1971.
Denne saken ble første gang publisert 21/06 2019, og sist oppdatert 21/06 2019.
